CBSE Class Class 12 Maths 2 Marks Important Questions for 2026 Board Exam

CBSE 12th Maths 2 Marks Questions: CBSE Class 12 Board Exams 2026 are approaching, and Mathematics continues to be a crucial subject for students in the Science and Commerce streams. Scoring well in Maths requires strong conceptual clarity, consistent practice, and smart problem-solving skills. Many students often struggle with accuracy and time management under exam pressure, even if they know the method.

To help students improve their overall performance, CBSE provides several essential study resources such as sample papers, marking schemes, and previous year question papers. Along with these, practising 2-mark questions is extremely important because they test core concepts in a concise format and contribute significantly to the overall score.

In this article, we bring you a curated list of the most important 2-mark questions for CBSE Class 12 Maths Board Exam 2026, based on repeated patterns in previous years’ board papers. Practising these questions will help students strengthen key topics, improve presentation skills, and enhance speed during the final exam.

List of 10 Important Questions of 2 Marks for Class 12th Maths with Solutions

Question 1: Find the domain of the function y = cos-1 (|x - 1|). Show your steps.

Answer: Since the domain of inverse of cosine function is [-1, 1], finds the domain of the given function as follows:

-1 ≤ x - 1 ≤ 1

So, 0 ≤ x ≤ 2

And,

-1 ≤ 1 - x ≤ 1

=> 1 ≥ x - 1 ≥ -1

So, 2 ≥ x ≥ 0

Concludes the domain of cos-1 (|x - 1|) as [0, 2].

Question 2: Iqbal, a data analyst in a social media platform is tracking the number of active users on their site between 5 pm and 6 pm on a particular day.

The user growth function is modelled by N(t) = 1000e 0.1t , where N(t) represents the number of active users at time t minutes during that period.

Find how fast the number of active users are increasing or decreasing at 10 minutes past 5 pm. Show your steps.

Answer: Write that the rate at which the number of active users is increasing or decreasing at a given time is given by d/dtN(t).

Finds the derivative of N(t) as: d/dtN(t) = 1000 (0.1) e^0.1t Finds the rate of change of active users at 10 minutes past 5 pm as: d/dtN(10) = 1000(0.1)e^(0.1)(10) = 100e

Concludes that the number of active users are increasing at a rate of 100e people per minute at 5:10 pm on that day.

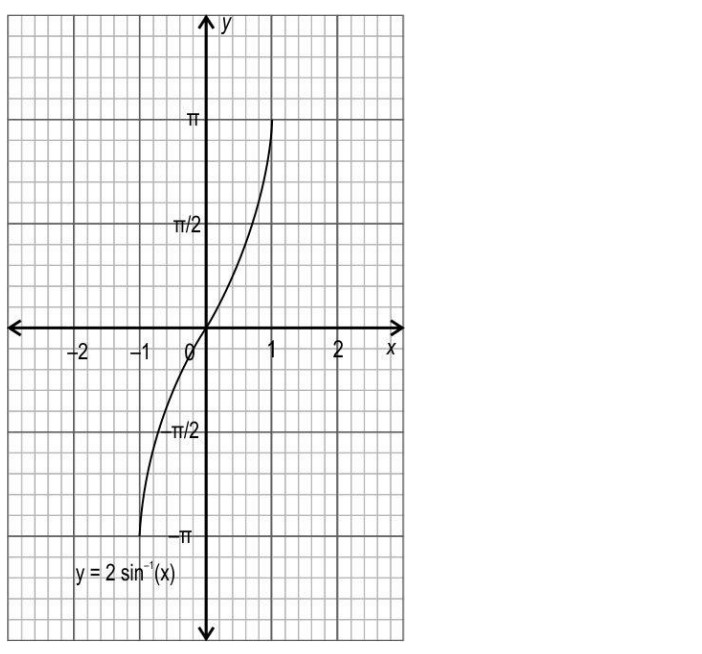
Question 3: Draw the graph of the following function: y = 2sin-1 (x), -π ≤ y ≤ π

Answer: Draws the graphs of y = 2sin-1 (x) as shown below.

Question 4:

i) What is the equation of this line in cartesian form?

ii) If A’s coordinates are (-2,5,-3), use the cartesian equation of the line to find the coordinates of B.

Answer: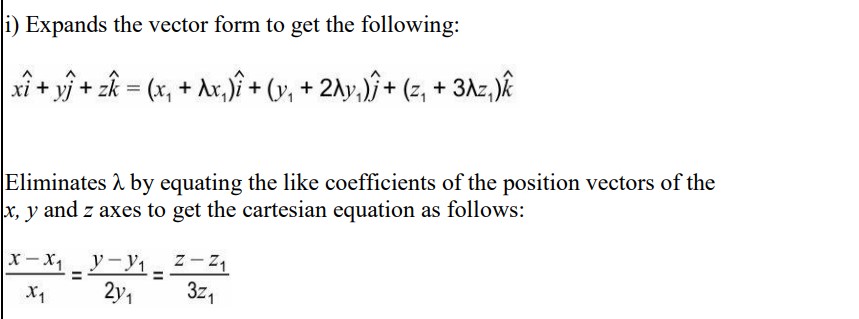

iii) Assumes the coordinates of B as (x₂,y₂,z₂) and compares the cartesian form of the equation from step 2 with the regular form of the cartesian equation to find: 

x₂=2x₁, y₂=3y₁ and z₂=4z₁

Substitute values x₁ = (-2), y₁ = 5 and z₁ = (-3) in the equations from step 3 to get coordinates of B as (-4, 15, -12).

Also Read: CBSE Class 12 Maths Board Exam 2024: Check 60 Day Study Plan and Weekly Strategy to Score 95+ Marks

Question 5: Based on the above equation, find tan^-1(1/x) using the principal values of the inverse trigonometric functions. Show your work.

Answer: Solves the RHS to obtain 2π/3 as follows:

cos^-1(-1)-cosec^-1(2/√3)

= π-π/3

= 2π/3

Equates the LHS to obtain x = − 1/√3 as follows:

cot^-1(x) = 2π/3

x=cot(2π/3)

x= -(1/√3)

Finds tan⁻¹(1/x) as -π/3 as follows:

tan^-1(1/x) = tan^-1(-√3)= -π/3

Question 6:

Answer:

i) Finds the domain as (−∞, 2/5] ∪ [ 4/5,∞)as follows:

5x-3≤-1 or 5x-3≥1

x≤2/5 or x≥4/5

ii) Finds the range as [−2,3π− 2] as follows:

0≤cos^-1(1/2x-1)≤π

3(0)-2≤3cos^-1(1/2x-1)-2≤3(π) -2

3(0)-2≤y≤3(π)-2

-2≤y≤3π-2

Question 7: If A is a square matrix such that A² = I, then find the simplified value of (A – I)³ + (A + I)³ – 7A.
Answer:

Given, A² = 7 ……. (i)

Now, (A – I)³ + (A + I)³ – 7A

= (A³ – 3A²I + 3AI² – I) + (A³ + 3A²I + 3AI² + I³) – 7A

= A³ – 3A² + 3AI – I + A³ + 3A² + 3AI + I – 7A

[∵ A²I = A² and I³ = I³ = I]

= 2A³ + 6AI – 7A = 2A² A + 6A – 7A [∵ AI = A]

= 2IA – A [from Eq. (1)]

= 2A – A = A [∵ IA = A]

Question 8: Find the maximum profit that a company can make, if the profit function is given by P(x)=72+42x-x², where x is the number of units and P is the profit in rupees.

Answer: For maxima and minima, P’(x)=0 => 42-2x=0

=> x=21 and P’’(x)= -2<0

So, P(x) is maximum at x=21.

The maximum value of P(x)= 72+(42x21)-(21)² = 513 i.e., the maximum profit is 513.

Question 9: Prove that if E and F are independent events, then the events E and F’ are also independent.

Answer: Given, E and F are independent events, therefore

⇒ PE( ∩ F) = P(E) P(F) …….. (i)

Now, we have,

P(E ∩ F’) + P(E ∩ F) = P(E)

P(E ∩ F’) = P(E) – P(E ∩ F)

P(E ∩ F’) = P(E) – P(E ) P(F) [using Eq. (i))

P(E ∩ F’) = P(E) [1 – P(F)]

P (E ∩ F’) = P(E ) P(F’)

∴ E and F ‘are also independent events.

Hence proved.

Question 10: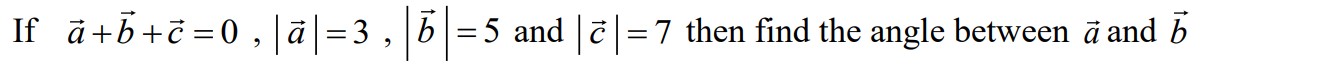

Answer: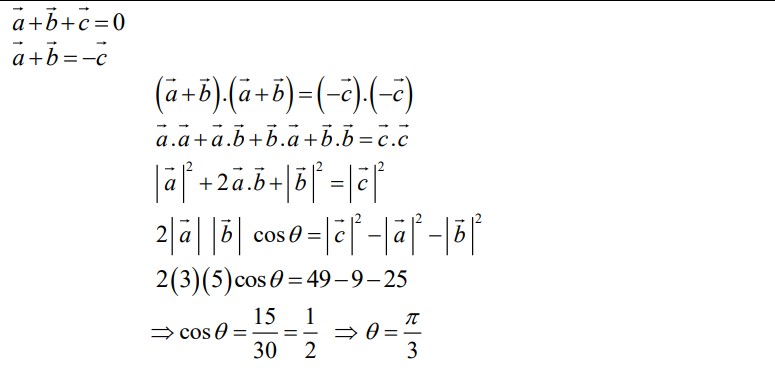

You can download the questions in PDF format below.

CBSE asks 5 very short answer-type questions in the board exam under 2 mark segment, The section has been named as Section B. Under this section, the board will ask short questions to students that can be answered within 10 minutes at maximum. 

Recommended: