The CBSE Class 12 Maths Half Yearly Sample Paper for 2025-26 is an essential resource for students preparing for their mid-term exams. This sample paper is designed to help them evaluate their knowledge of the Mathematics syllabus, including topics like Calculus, Algebra, Vectors, and Probability. By practicing with this resource, students can familiarize themselves with the exam format, manage their time effectively, and identify the types of questions they might face.
This sample paper serves as a valuable tool for students aiming to score well in their exams, typically held in September or October. It provides a clear overview of the exam pattern and helps students gain confidence by allowing them to self-assess their preparation. Using this resource is a convenient way to revise coursework and focus on areas that need improvement before the actual examination.
CBSE Class 12 Maths Units and Weightage (2025-26)
The CBSE Class 12 Maths curriculum majorly divided into different sections which are as follows:
| No. | Units | Marks |
| 1. | Relations & Functions | 08 |
| 2. | Algebra | 10 |
| 3. | Calculus | 35 |
| 4. | Vectors and Three - Dimensional Geometry | 14 |
| 5. | Linear Programming | 05 |
| 6. | Probability | 08 |
| Total |
| 80 |
|
| Internal Assessment
| 20 10 10 |
| Grand Total |
| 100 |
CBSE Class 12 Maths Term 1 Sample Paper 2025-26
Class -XII
Subject – Mathematics (041)
Max. Marks - 80
Max. Time – 3 Hrs.
General Instructions:
-
This question paper contains 38 questions divided into three sections- A, B, C & D
-
All questions are compulsory.
-
Section - A contains 20 very short answer type (VSA) of 1 mark each.
-
Section - B contains 5 short answer type (SA-I) questions of 2 marks each.
-
Section - C contains 6 short answer type (SA-II) of 3 marks each.
-
Section -D contains 4 long answer type questions (LA) of 5 marks each.
-
Section -E contains 3 case based questions (CBQ) of 4 marks each.

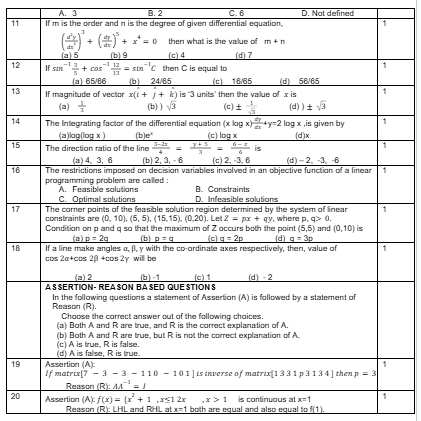
SECTION-B | ||
| 21 | Find the principal value of cos 13π6. OR Find the value of(3) --2. | 2 |
| 22 | If x=a tan3θ and y=a sec3, then find dydx . | 2 |
| 23 | Evaluate : sec2xtan2x+4dx OR 1-sin 2x dx, 4<x<2. | 2 |
| 24 | If a =2, b =7 and a b =-3i+j+2k, find the angle between a and b . | 2 |
| 25 | Let X be a random variable which assumes values x1, x2, x3, x4 such that 2PX=x1=3PX=x2=PX=x3=5PX=x4. Find the probability distribution of X. OR A die, whose faces are marked 1, 2, 3 in red and 4, 5, 6 in green is tossed. Let, A be the event “number obtained is even” and B be the event “number is marked red”. Find whether the events A and B are independent or not. | 2 |
SECTION C | ||
| Sl. No. | Question | Marks |
| 26. | Let X denote the number of hours you study during a randomly selected school day. The probability that X can take the values x, has the following form, where k is some unknown constant.
| 3 |
| 27. | Evaluate 5x+3x2+4x+10dx | 3 |
| 28. | Solve the differential equation (y –x)dy=(1+y2)dx. OR Show that the family of curves for which the slope of the tangent at any point (x,y) on it is x2+y22xy, is given by x2-y2=cx | 3 |
| 29. | Evaluate 04sin x+cos x 9+16sin 2x dx OR Evaluate 04x+x-2+x-4dx | 3 |
| 30. | If y=ex , -1≤x≤1, show that1-x2d2ydx2-x dydx-m2y=0 | 3 |
| 31. | Find the maximum value of Z = 3x + 4y subjected to constraints x + y ≤ 40, x+ 2y ≤ 60, x ≥ 0 and y ≥ 0. OR Find the point where the minimum value of Z occurs : Z=2x+y, subject to constraints 3x + y ≥ 9, x + y ≥ 7, x + 2y ≥ 8, x ≥ 0, y ≥ 0. | 3 |
SECTION D | |||
| Sl.No. | Question | Marks | |
| 32 | If A = 2 3 1 -3 2 1 5 -4 -2 , find A-1 and use it to solve the system of equations: 2x – 3y + 5z = 11, 3x + 2y – 4z = - 5, x + y – 2z = - 3 | 5 | |
| 33 |
| 5 | |
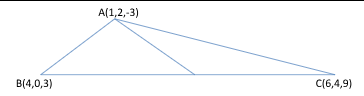
| 34 | If A(1,2,-3) , B(4,0,3) and C(6,4,9) be the vertices of triangle ABC . If AD be the median then Find (i)Equation of side BC (ii) Equation of Median AD (iii)Angle between AD and BC.(2+3 marks)
OR Find equation of line which passes through (1, 1, 1) and perpendicular to both the following lines x-12=y-23=z-34 and x+21=3-y-2=z+14. | 5 | |
| 35 | Using integration find the area of region bounded by 2x-y+2=0, x=-2, x=3 and x axis. | 5 | |
SECTION E | ||
| Sl.No. | Question | Marks |
| 36 | The reliability of a COVID PCR test is specified as follows: Of people having COVID, 90% of the test detects the disease but 10% goes undetected. Of people free of COVID, 99% of the test is judged COVID negative but 1% are diagnosed as showing COVID positive. From a large population of which only 0.1% have COVID, one person is selected at random, given the COVID PCR test, and the pathologist reports him/her as COVID positive Based on the above information, answer the following (i) What is the probability of the ‘person to be tested as COVID positive’ given that ‘he is actually having COVID? (ii) What is the probability of the ‘person to be tested as COVID positive’ given that ‘he is actually not having COVID’? (iii) What is the probability that the ‘person' is actually having COVID given that ‘he is tested as COVID positive’? | 4 |
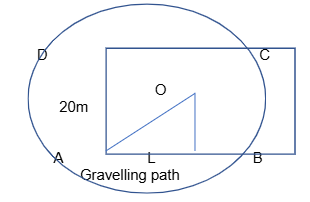
| 37 | An architect designs a garden in a residential complex. The garden is in the shape of a rectangle inscribed in a large circle of radius 20 m as shown in the following figure. If the length and breadth of rectangle garden are 2x and 2y meters respectively.
Based on the above information answer the following (i) find the area A of the green grass of garden also find dAdx (ii) find the maximum area of the garden. | 4 |
| 38 | Ishaan left his village on the weekend. First, he travelled up to the temple. After this , he left for the Zoo. After this, he left to go shopping in a mall. The position of Ishaan at different Places is given in the following graph Based on the above information, answer the following (i) find the position vector of B and D in term i & j (ii) find the length of vector AD . (iii) find the vector BC . and if M =4 j+3 k then find the unit vector of M . | 4 |
CBSE Class 12 Maths Half Yearly Sample Paper 2025-26: Answer Key
SECTION A | ||
| Sl. no. | Answer | Marks |
| 1 | D | 1 |
| 2 | A | 1 |
| 3 | C | 1 |
| 4 | A | 1 |
| 5 | B | 1 |
| 6 | D | 1 |
| 7 | A | 1 |
| 8 | C | 1 |
| 9 | D | 1 |
| 10 | B | 1 |
| 11 | A | 1 |
| 12 | D | 1 |
| 13 | D | 1 |
| 14 | C | 1 |
| 15 | C | 1 |
| 16 | B | 1 |
| 17 | B | 1 |
| 18 | B | 1 |
| 19 | D | 1 |
| 20 | A | 1 |
SECTION B | ||||||||||||
| Sl.No. | Answer | Marks | ||||||||||
| 21 | We know that, cos x =x, if x0, . Now, cos 136 =cos 2+6 , ∵ 1360, =cos 6 , ∵cos 2+x=cos x =6, ∵60, OR (3) --2 =3--2 , ∵-x=-x =3--3 =3-23 =-3 | 2 2 | ||||||||||
| 22 | x = a tan 3 θ Differentiating w.r.t. θ dxdθ = a 3 tan2 θ sec2 θ Again, y = a sec3 θ Differentiating w.r.t. θ dydθ = a 3 sec2 θ sec θ tan θ = 3 a tan θ sec3 θ dydx = dydθdxdθ=3 a tan θ sec3 θ/ a 3 tan2 θ sec2 θ = sec θ tan θ = cosec θ | 2 | ||||||||||
| 23 | sec2xtan2x+4dx Let,tan x=z ∴sec2x dx=dz =dzz2+22 =log z+z2+22+c =log tan x +tan2x+4+c OR 1-sin 2x dx, 4<x<2 =sin2x+cos2x-2.sin x .cos x dx =sin x -cos x 2dx =sin x -cos x dx, in 4<x<2, sin x is greater than cos x =-cos x -sin x +c | 2 | ||||||||||
| 24 | a b =a b sin θ n , where n is a unit vector. a b =a b sin θ n -32+12+22=a b sin n 9+1+4=2.7.sin .1 14=14 sin 1414= sin 114= sin sin =114 sin =±114 θ=114 | 2 | ||||||||||
| 25 | Let, 2PX=x1=3PX=x2=PX=x3=5PX=x4=k ∴PX=x1=k2, PX=x2=k3, PX=x3=k, PX=x4=k5 Now, PX=x1+PX=x2+PX=x3+PX=x4=1 k2+k3+k+k5=1 15k+10k+30k+6k30=1 61k30=1 k=3061
OR S=1, 2, 3, 4, 5, 6 A= 2, 4, 6 B=1, 2, 3 A∩B=2 PA=36=12 PB=36=12 PA∩B=16 PA.PB=12.12=14 ∴PA∩B≠PA.PB Hence,A and B are not independent | 2 2 | ||||||||||
| SECTION C | ||
| Sl.No. | Answer | Marks |
| 26 | The probability distribution of X is | 3 |
| 27 | | 3 |
| 28 | | 3 |
| 29 | OR For correct solution = 20 | 3 |
| 30 | (1-x2)dydx =my Again diff. w.r.t. x and solve we get | 3 |
| 31 | Maximum value = 140 OR From the table, we find that 8 is the minimum value of Z at G(1, 6). Since the region is unbounded we have to check that the inequality 2x + y < 8 in the open half plane has any point in common or not. Since, it has no point in common. So, Z is minimum at G (1, 6) and the minimum value of Z is 8. | 3 |
| SECTION D | ||
| Sl.No. | Answer | Marks |
| 32 | | 5 |
| 33 | | 5 |
| 34 | OR | 5 |
| 35 | | 5 |
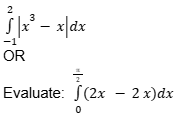
Comments
All Comments (0)
Join the conversation